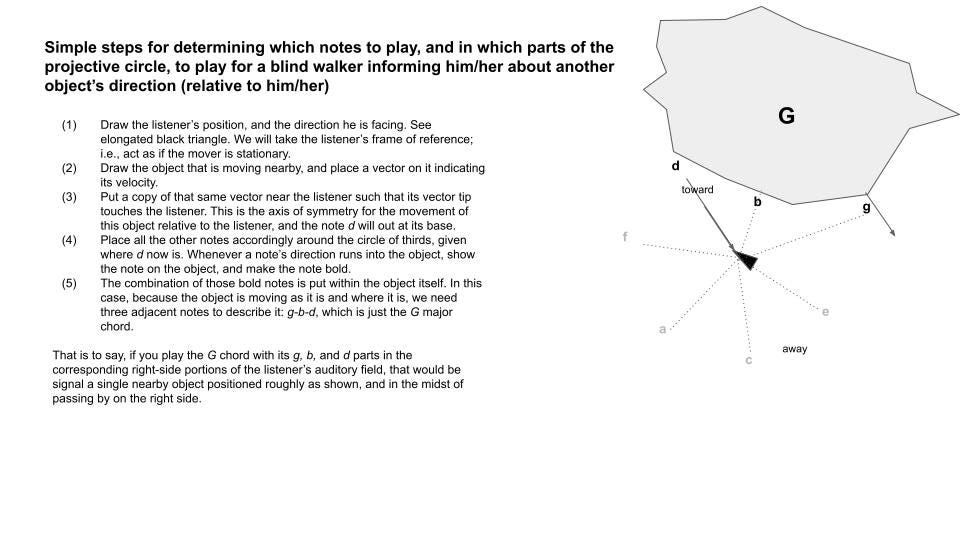
Musical chords and the movement of nearby objects
...and a new idea for augmented hearing for the blind.
I’ve been working since May on some new ideas on the foundations of music, in particular trying to understand what chords and chord progressions mean to our brains. My earlier book, HARNESSED, covered the origins of many facets of music, but not chords. (See the end of this piece for links to recent posts.)
My suspicion has been that chords tell your brain about the directions of movement of objects around you, but I hadn’t yet made much sense of the differing sizes of chords.
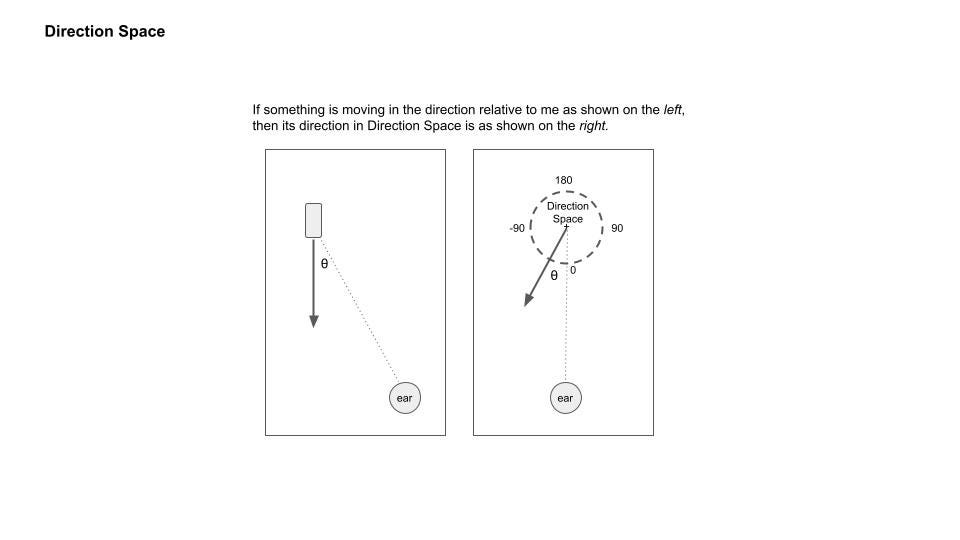
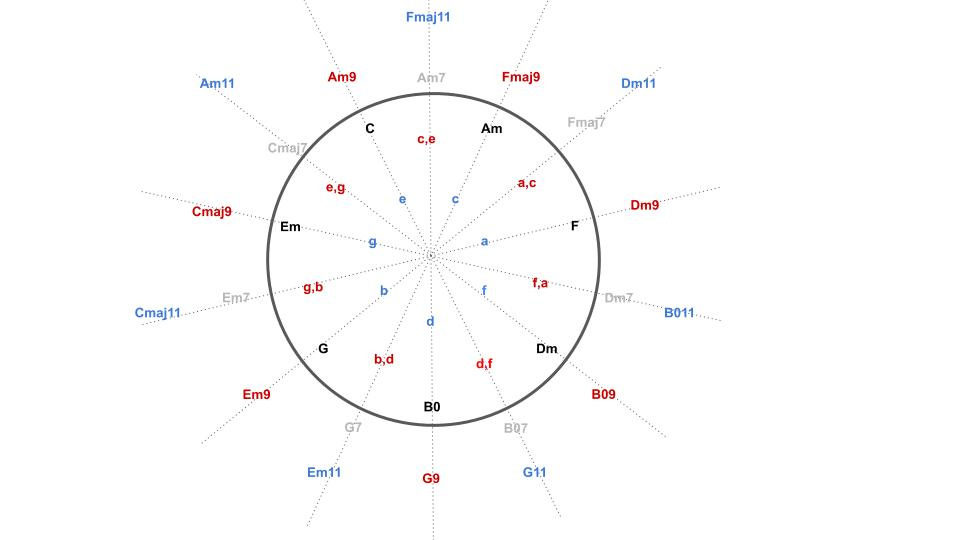
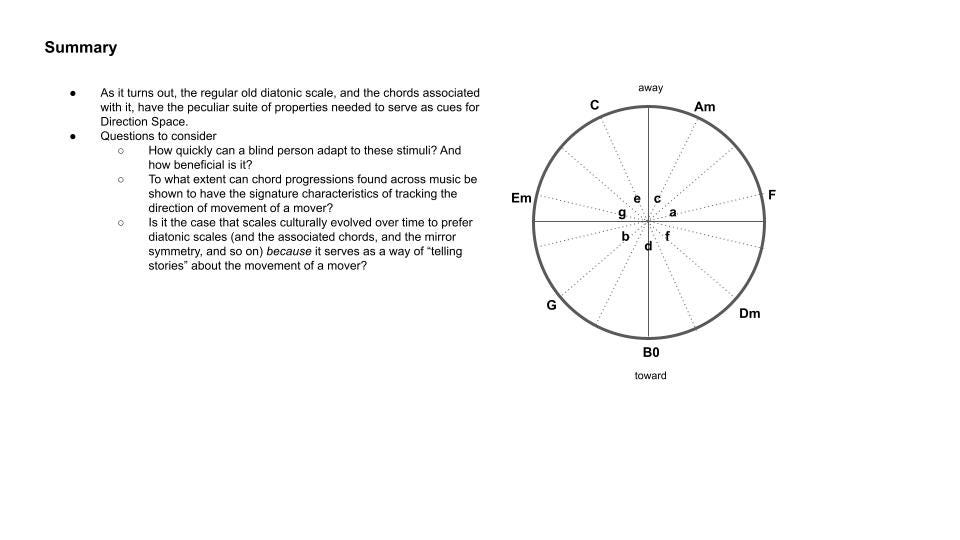
Below you can see the space (chord space, or direction space) we had built up to.
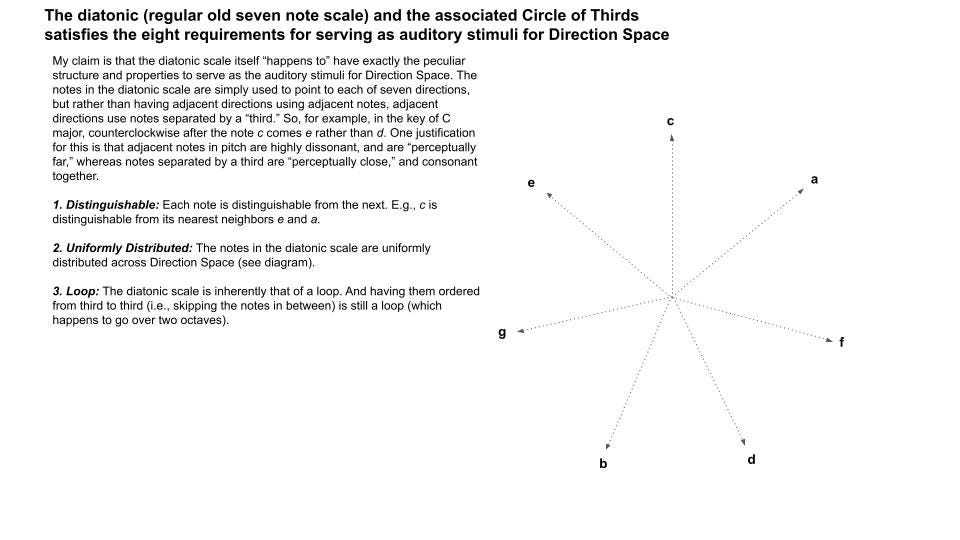
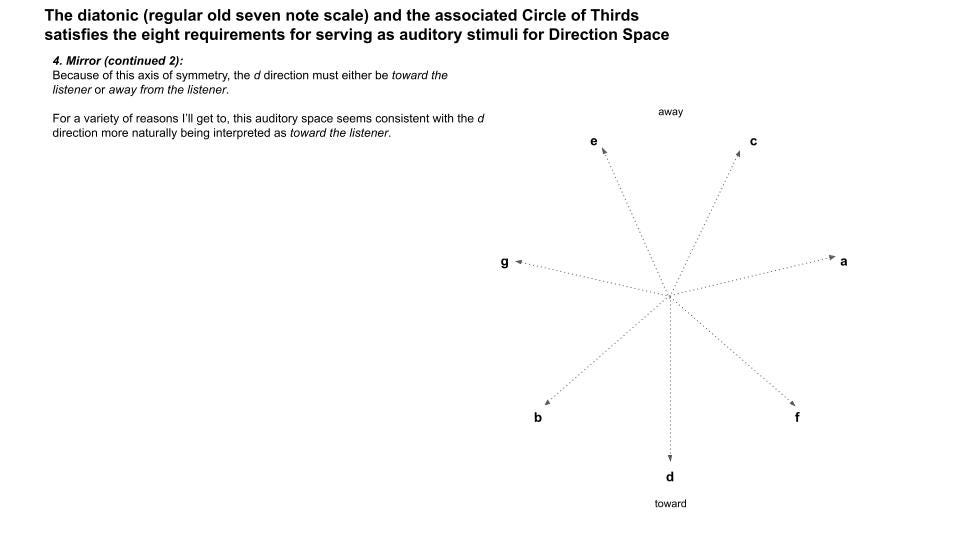
It begins with the blue notes near the center, which is just the Circle of Thirds, beginning on, say, c, and jumping by thirds all the way across the keyboard until you’re back again to c. So, c, e, g, b, d, f, a, and to c again.
The justification for nearby directions in this space being these thirds rather than adjacent notes in the key (of C) is that moving from a note to its immediate neighbors leads to a note that is highly dissonant when played together with the first. But jumping by thirds leads to a highly consonant note.
Another justification is that, when you do do it this way, you can naturally represent adjacent pairs (the red pairs shown), regular triads (in black), the sevens (gray), nines (red) and elevens (blue).
They each have well-defined positions in the space.
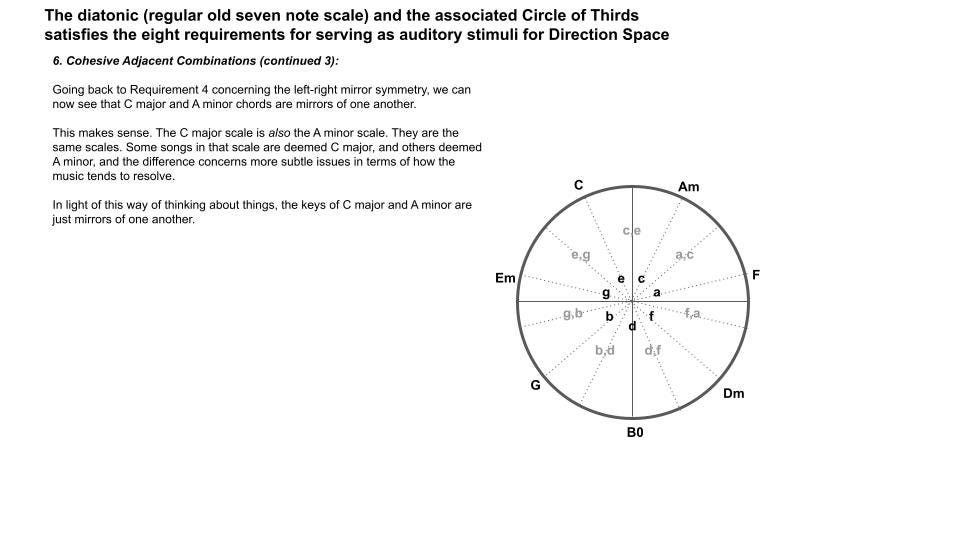
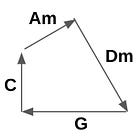
And, for the triads — the backbone chords in music — this space is a metric, which is to say, if two triad chords are adjacent in this space above, it means there is a single note change that brings us from one chord to the other. Such as Am to C via changing g to a.
Anyhow, the space above is, as far as I know, the first time the full range of standard chords (and their generalization) within a key have been visualized in one diagram.
And, as I said, my suspicion has been that this space is actually telling our brains during the music about the direction of movement of the human mover.
But, one mystery has been, why are there chords of differing sizes at the same spot in direction space? For example, e, C and Am9 are all at the same direction in the space. What’s the difference?
Recently I had a key insight that might answer this.
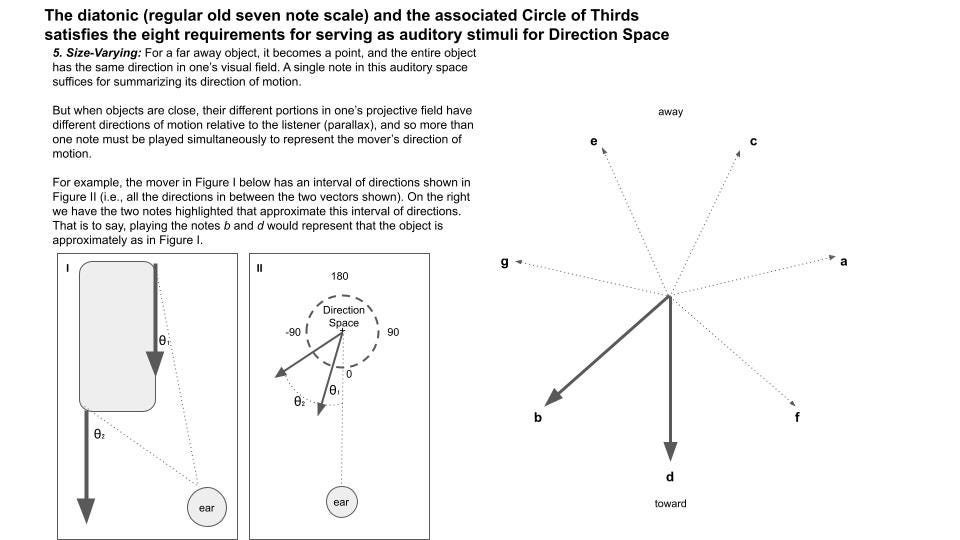
When an object is far away, a single direction characterizes its movement relative to you. It’s far, and so is basically a single point.
But…
When an object is nearby, it fills up an appreciable portion of your visual field. (Let’s call it your projective field, as we’re not talking about vision here.)
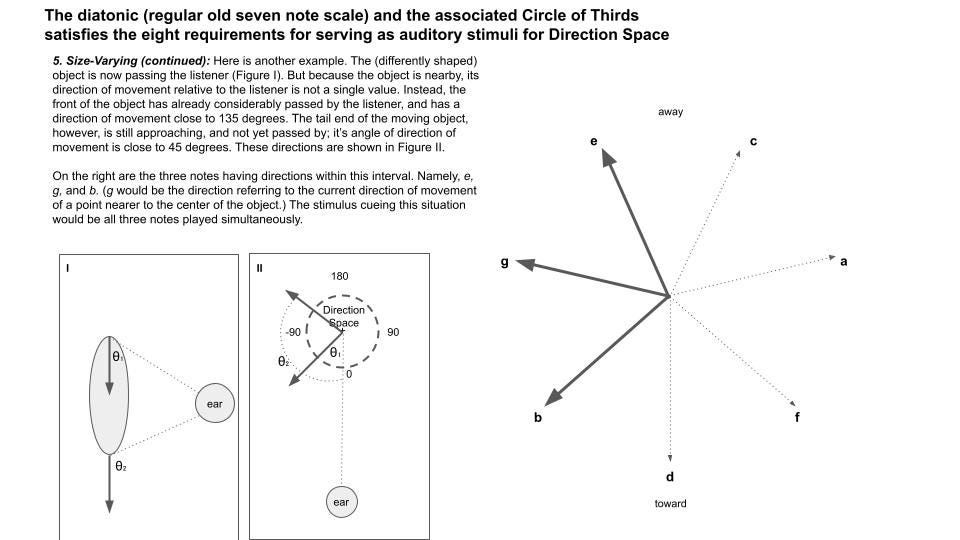
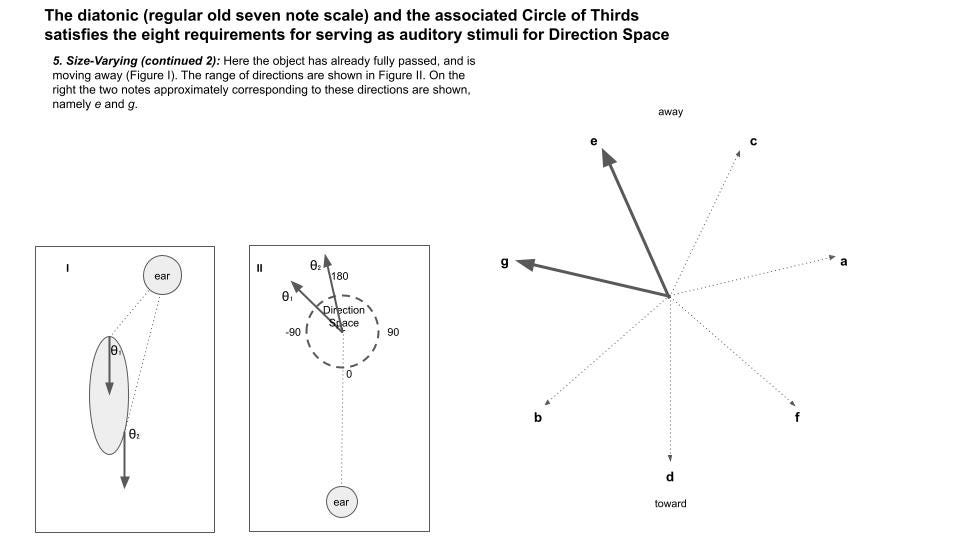
And so… it immediately follows that for a nearby moving object, different parts of it are moving at different directions relative to you. This is just called parallax.
For example, suppose a bus is passing you very closely. At the moment it is passing, its front is moving largely away from you — it’s already passed. Its tail end, however, is still approaching.
For vision, we use these differences in movement direction on different parts of the scene (parallax) to determine the three dimensional structure of objects or the environment.
But chords can allow our auditory system to do this! …
A single chord sounds like one cohesive thing, yet it informs the brain about multiple distinct directions of movement of that one thing.
If this is correct, then when music is doing just, say, single note “chords,” it’s indicating that the mover is far away.
But as the mover gets closer, the chords get larger. Or, said the other way around, the larger the chord, the more your brain thinks the mover is nearby. It’s more dramatic. And the sequence of chords informs your brain about the manner in which the object is moving in your midst, with considerable parallax information embedded in those chord progressions.
I have lots of work to do to flesh out a case for this, but the idea even as is might be useful for applications for the blind, which I walk through in this sequence of slides…