Can Music Let Blind People "See"?
Music culturally evolved to harness our human-movement recognition system. Here I show you how we might be able to harness music to help blind people better perceive the world around them.
In my 2011 book, Harnessed: How Language and Music Mimicked Nature and Transformed Ape to Man, I argued that music has culturally evolved to sound like a human evocatively moving in your midst.
Recently I began wondering: If music encodes movement, might we be able to use music to help blind folks who have a profound difficulty with movement. Might it be possible to use music to encode how the world around them moves as they move, and thereby give them an “auditory sight” of sorts?
The answer might be Yes. Here I will show that musical notes and chords “happen” to have all the needed properties to serve the role as auditory augmentation for the blind. (And I suspect it’s no accident, although my case for that is in the works, perhaps as a Harnessed II.)
In this write-up I’ll run through the basic idea.
I’ll describe key properties an auditory augmentation system of this kind needs to possess.
I’ll then show how the seven-note scale (and its Circle of Thirds) has exactly the needed properties.
I’ll then describe how to use the idea to help the blind perceive the world around them as they move within it.
A. Moving Experience
It’s relatively straightforward to use sound to replace the visual system’s ability to identify where, or in which direction, things might be. One just needs something like a fancy helmet that plays a sound at a position corresponding to where something is around you. If there’s a pillar 30 degrees to the right, the helmet can activate a speaker at that position. Nowhere near the resolution eyes give you, but you get the idea. And it would be great.
But having information about where things are isn’t enough. When you see the world, you’re not only seeing where things are, but also simultaneously seeing how things in the world are moving relative to you.
You see movement too.
And the movement you experience is not because your brain is inferring it by analyzing a sequence of wheres. No. You have motion-specific visual neurons in your eyes. You sense the motion itself, and without that you couldn’t possibly competently move and navigate the world.
To really provide an auditory replacement for vision for the blind, we need to provide an auditory experience that doesn’t just provide the where, but also informs the blind person of the direction of movement of things in the world.
Is it possible to use auditory stimuli to inform perception of the direction of movement of things around us, and not just where the things are?
Before actually providing my idea about what kind of auditory stimuli might work for this, I’m first going to walk you through what we need those auditory stimuli to actually do for us. The perception of movement of things relative to your position has certain simple properties that it’s important to flesh out so that we can more carefully make sure that my auditory augmentation idea is up to the task.
B. Eight Things Auditory Augmentation Should Do
Any object around you can be moving in any direction relative to you. Figure 1 illustrates Movement Space, which is just the space of all the different directions an object can move relative to you (along the ground).

If we wish to allow blind people to perceive the movements of objects around them, then we need to somehow use sounds to encode Movement Space.
Of course, you already know that I’m going to argue we can do it via music in some way, but for now I just want to focus on some of the key things our auditory stimuli for this must satisfy.
1. Distinguishable
There must be distinguishable auditory stimuli associated with many directions within Movement Space. That is just to say, we need to be able to tell apart the sounds for each direction of movement.
2. Uniformly Distributed
The auditory stimuli must be approximately uniformly distributed across Movement Space. Said differently, we want distinct sounds across many different directions an object might be moving relative to you, and we don’t really want some directions to have greater resolution than others.
3. Loop
The auditory stimuli must go in a loop, i.e., from 0 deg to 360 deg. That is to say, objects can move in any direction (along the ground) relative to your position, and that’s just all the directions in a circle.
4. Mirror
Movement Space is left-right symmetric, i.e., the range from 0 to 180 deg is mirror-symmetric with the range from 0 to -180. Therefore, any auditory stimuli we might concoct for blind people for this space must also be left-right symmetric.
5. Size-Varying
For an object very far away, we can treat it as a point, and its direction of movement is characterized by a single direction in Movement Space.
But when an object is nearby and fills a considerable portion of your projective field (i.e., it blocks a lot of your view), not only are the different portions of the object at different positions around you, but the different portions of the object are moving in different directions relative to you. See Figure 2 for an example.
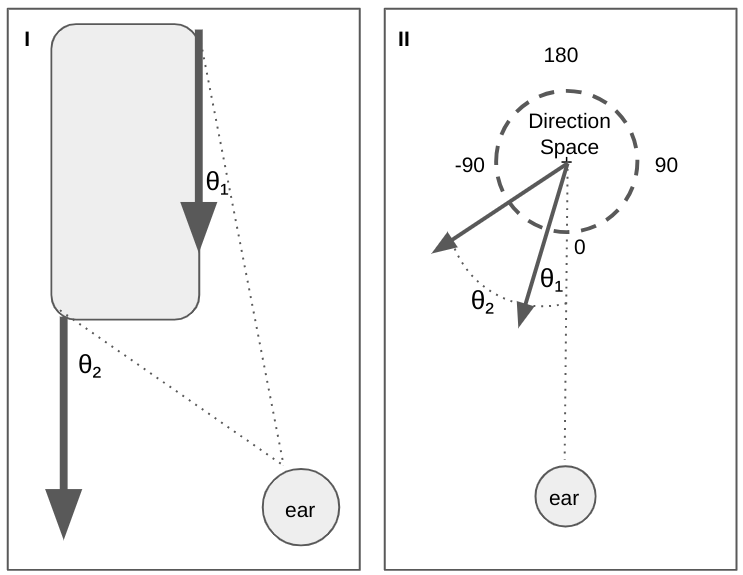
This is crucial for the perception of the direction of movement of objects. The name for this is parallax.
Nearby objects must present as multiple simultaneous distinct auditory stimuli.
Said another way, to characterize the movements of objects around you, we will need multiple simultaneous sounds (in multiple spots around you), because single objects actually move in multiple simultaneous directions relative to your position.
(All the object’s parts are obviously moving in the same direction relative to the world, namely south in Figure 2. But we’re interested in the movement directions relative to your position.)
6. Cohesive Adjacent Combinations
Because the stimulus cue for the direction of a nearby object must be multiple simultaneous auditory stimuli (as we just discussed in 5), we must choose auditory stimuli such that they can combine and be meaningfully processed as a single sensible stimulus.
This is especially so for the auditory stimuli for similar directions, as they will end up combining more often.
On the other hand, directions that are very different (e.g., 180 degrees apart) need not easily perceptually combine, and might instead be dissonant (or clash), as they are much more inconsistent with the movement of a single object.
7. Associations
Whether objects are coming toward you, passing you, or moving away from you, matters a lot in terms of its implications. Objects moving toward you are more worth your attention, and they only come toward you for so long, after which they pass you. Moving away from you is comparatively stable, unless the mover “chooses” to turn around and come back toward you. The auditory stimuli associated with these distinct qualitative kinds of movement directions should instinctively connote these differences.
8. Meaningful Sequential Combinations
It’s not just that your brain must be able to process the multiple sounds for the multiple directions an object is moving (relative to you), but that object moves for an extended period of time in your vicinity, and so the sequence of these sound-combinations — which represents the object’s movement over time — needs to be sensible and interpretable to your brain.
C. Music satisfies these eight constraints
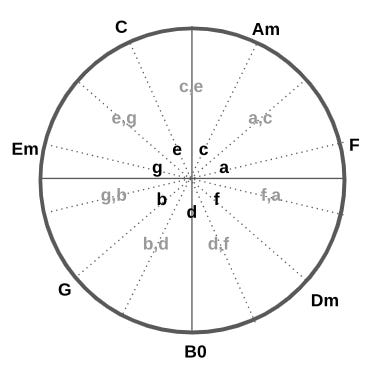
My claim is that the regular old seven note scale you’re familiar with — the “diatonic scale” — happens to have exactly the peculiar structure and properties needed to serve as the auditory stimuli for Movement Space. In particular, the notes in the diatonic scale are used to point to each of seven directions, but rather than having adjacent directions using adjacent notes in the scale, adjacent directions use notes separated by a “third.” See Figure 3.
So, for example, in the key of C major, counterclockwise after the note c comes e rather than d. After e comes g rather than f. And so on around the circle until a brings us (skipping b) back to c.

One a priori justification for this is that adjacent notes in pitch (like c and d) are highly dissonant, and so are actually “perceptually far,” whereas notes separated by a third are “perceptually close,” and consonant together.
This sounds suspiciously over-simple. How can a mere seven notes strewn in thirds around the circle possibly serve to satisfy all eight constraints we just discussed?
Let’s walk through them one by one.
1. Distinguishable
Each note in the seven-note scale is distinguishable from every other.
2. Uniformly Distributed
The notes in the diatonic scale are indeed uniformly distributed across Movement Space (see Figure 3).
3. Loop
The diatonic scale is inherently that of a loop. And having them ordered from third to third (i.e., skipping the notes in between) still makes a loop (which happens to go over two octaves before getting back to the start).
4. Mirror
The Circle of Thirds (Figure 3) has the needed mirror symmetry, although it is not often appreciated that this is the case.
To see that there’s a mirror symmetry within it, I have placed “major” and “minor” between each interval in Figure 4 below. “Major” means that there are four semitone steps (the smallest steps from note to note on a piano, using the full 12 note scale) separating the notes, and “minor” means there are three semitone steps. For example, from c to e is c-c#-d-d#-e (a major interval, or four steps), but from e to g is e-f-f#-g (a minor interval, or three steps).
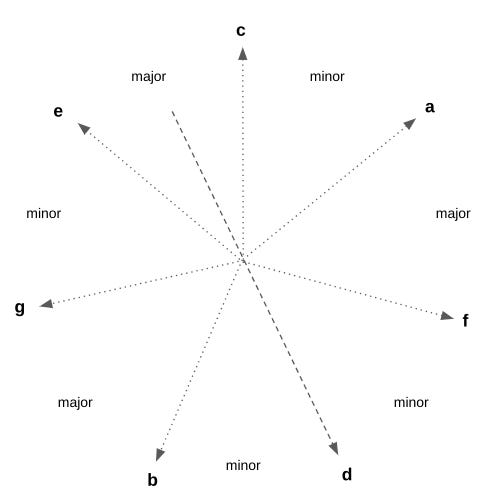
If you examine the space with these “major” and “minor” labels, you will see that there is exactly one axis of symmetry such that there is a left-right symmetry across it. It’s the axis that goes through the note d (shown in Figure 4 as the dashed line).
The Circle of Thirds above has now been rotated a little clockwise so that the axis of symmetry is vertical, as shown in Figure 5 below.

In terms of the diatonic scale, this symmetry is due to the unique position of d within the diatonic scale it’s part of. It’s the only note for whom “looking to the left” looks the same as “looking to the right” on the keyboard.
Said differently, consider c on the piano shown in the upper portion of Figure 6 below. The lower image below it shows that same image except that it has been flipped horizontally. Now the c note is actually the e in this reflection. Similarly, g and a are mirrors of one another, as are b and f. You can see that these mirrors are on opposite sides of the diagram in Figure 5.
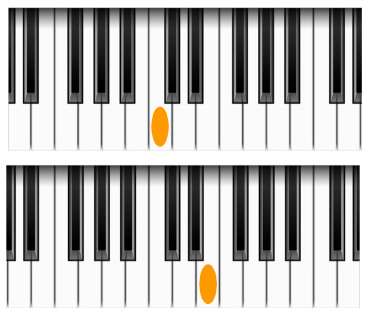
Because of this axis of symmetry, the d direction must either be toward the listener or away from the listener.
For a variety of reasons I’ll get to, this auditory space seems consistent with d more naturally being interpreted as toward the listener.
5. Size-Varying
For a far away object, it becomes a point, and the entire object has the same direction in one’s visual field. A single note in this auditory space therefore suffices for summarizing the object’s direction of motion.
But when objects are close, their different portions in one’s projective field have different directions of motion relative to the listener, as we discussed, and so more than one note must be played simultaneously to represent the object’s direction of motion.
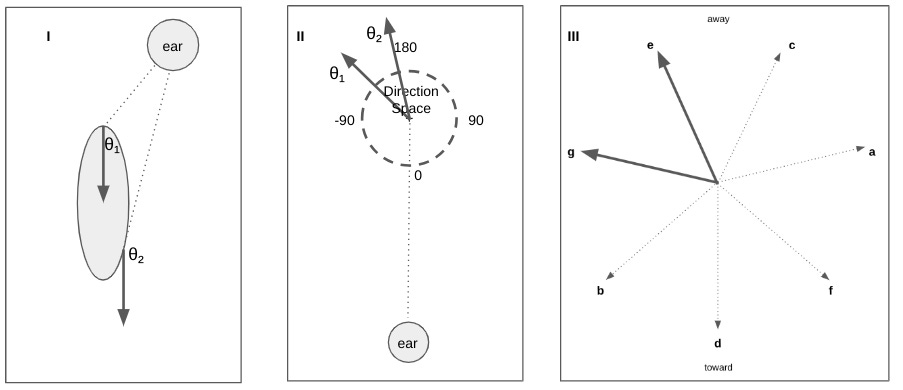
For example, the moving object in Figure 7-I below has an interval of movement directions shown in Figure 7-II (i.e., all the directions in between the two vectors shown). On the right (in Figure 7-III) we have the two notes highlighted that approximate this interval of directions. That is to say, playing the notes b and d would represent that the object is approximately as in Figure 7-I.

Here is another example. The (differently shaped) object is now passing the listener (Figure 8-I). But because the object is nearby, its direction of movement relative to the listener is not a single value. Instead, the front of the object has already considerably passed by the listener, and has a direction of movement close to 135 degrees. The tail end of the moving object, however, is still approaching, and not yet passed by; it’s angle of direction of movement is close to 45 degrees. These directions are shown in Figure 8-II. On the right (Figure 8-III) are the three notes having directions within this interval. Namely, e, g, and b. (g would be the direction referring to the current direction of movement of a point nearer to the center of the object.) The stimulus cuing this situation would be all three notes played simultaneously.

Figure 9-I shows a case where the object has already fully passed, and is moving away. The range of directions are shown in Figure 9-II. On the right (Figure 9-III) the two notes approximately corresponding to these directions are shown, namely e and g.
6. Cohesive Adjacent Combinations:
The issue here is, if these notes, each coding for a distinct direction of movement, are played simultaneously, is the resultant sound something that our brain can make sense of?
Yes!
Adjacent combinations of these notes give us exactly the ranges of chords used in music!
First, combining any two adjacent notes in this space just leads to two-note pairs, and such notes, as they are separated by a third, always sound consonant, as if it’s due to one “thing” in the world. Each of the seven pairs are shown in gray in Figure 10, and each is placed in the direction at the center between the two individual directions. (However, remember that that’s not the direction of the object a two-note pair describes. Rather, a two-note pair concerns a single relatively nearby object, describing the range of directions of movement (relative to the listener) it possesses.)

Now consider when an object is even closer, and three notes must be used to describe its direction of movement. Now we have combinations of three of these adjacent note-directions. And these are simply the standard seven chords in the diatonic scale, shown below, placed at the centerpoint of their three directions in Figure 11. (But, again, the chords don’t indicate a single direction of movement, but the range of directions described by the notes within it.)
So, we have the C major chord, which is the combination of c, e, g, and then the Am chord, which is a, c, e, and so on. B0 refers to Bdim, or B diminished, which is b, d, f.

If instead we combine four adjacent notes for when objects are even closer, filling an even larger portion of the projective field, and having accordingly more widely diverse movement directions within it, we get the “sevens” chords now shown in gray in Figure 12. The dotted curve at the top shows the actual extent of the movement directions filled by Am7, as it includes a, c, e, g. All the sevens chords are similarly large, almost covering half of the space.

Via a similar process, the “nines,” “elevens” and “thirteens” chords occur for objects even closer, although all these large chords cover more than half of Movement Space, and aren’t generally ecologically possible (which is why they might be relatively rare in music). See Figure 13 for all them in one diagram. As far as I know, this is the first time all the chords in a key have been systematically shown in a single diagram.

Going back to Requirement 4 concerning the left-right mirror symmetry, we can now see that C major and A minor chords are mirrors of one another. This makes sense. The C major scale is also the A minor scale; they are the same scales. Some songs in that scale are deemed C major, and others deemed A minor, and the difference concerns more subtle issues in terms of how the music tends to resolve. In light of this way of thinking about things, the keys of C major and A minor are just mirrors of one another.
7. Associations
Do these chords have any associations that suggest they might actually be interpreted by the brain as directions of movement (relative to the listener)?
This may require another book length study to fully flesh out (a follow-up to Harnessed), but there are a variety of hints that it does.
For one thing, it is well known that certain chords have a strong “desire” to move to some, but not other, chords.
At the highest level, chords in C major have a tendency to go from C to F to G and back to C again. This is often called tonic to subdominant to dominant and back to tonic.
More generally, the tonics are C (and Am), and are deemed very stable, not “asking” for anything per se to happen next. This is consistent with them cuing moving away from the listener, because that is the stable situation for all movers.
Subdominants refer to F (and Dm), and are beginning to ask a question. Something has begun to happen. And it’s transient. This is consistent with the mover having turned from moving away to a transverse direction perhaps on its way to turn more directly toward you.
Dominants tend to come after subdominants, and refer to G and B0. They are dramatic. Lots of tension. It can’t last for too long. This is consistent with objects moving toward you, where eventually it will pass by (if it doesn’t hit you). …at which time it very rapidly goes back to the tonic, as it takes only a short period of time to begin moving away if the pass was nearby.
The dominant B0, if you re-check the earlier diagram with “major” and “minor” intervals shown between each note, consists of two minor intervals, rather than one major and one minor interval as all the other chords. This tends to make it sound more dissonant. More alarming. More looming. More temporary.

8. Meaningful Sequential Combinations
Not only do simultaneous combinations of the note-directions sound meaningful and cohesive, and not only might they have many associations with movement, but the sequential combinations of these chords are meaningful. Most music is built on the backbone of these. Their called chord progressions!
That is just to say, There’s no worry about whether people can reliably process and distinguish complex sequences of these stimuli.
How to determine which notes (which chord) to play
Here are simple steps for determining which notes to play, and in which parts of the listener’s projective circle, to inform her about an object’s direction (relative to her position).
Draw the listener’s position, and the direction she is facing. See elongated black triangle. We will take the listener’s frame of reference; i.e., act as if the mover is stationary.
Draw the object that is moving nearby, and place a vector on it indicating its velocity.
Put a copy of that same vector near the listener such that its vector tip touches the listener. This is the axis of symmetry for the movement of this object relative to the listener, and the note d will out at its base.
Place all the other notes accordingly around the circle of thirds, given where d now is.
Whenever a note’s direction runs into the object, show the note on the object, and make the note bold.
The combination of those bold notes is put within the object itself.

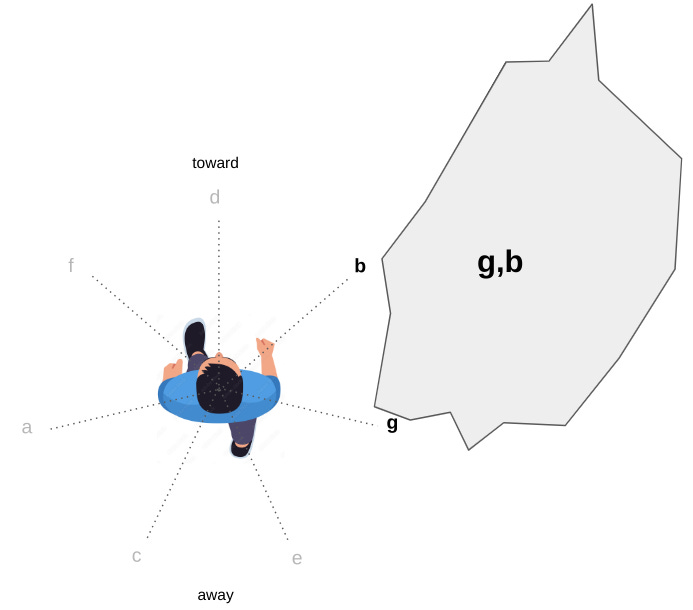
In the example shown in Figure 16 above, because the object is moving as it is and where it is, we need three adjacent notes to describe it: g-b-d, which is just the G major chord. That is to say, if you play the G chord with its g, b, and d parts in the corresponding right-side portions of the listener’s auditory field, that would signal a single nearby object positioned roughly as shown, and in the midst of passing by on the right side.
In the example shown in Figure 17 above, the object is now going to pass on the left side. It is currently far enough away that only the note f points to any part of the object. So only the f note will be played, and played in that particular listener position (on the listener’s front left side).
In Figure 18 above, the object is now on the listener’s right (and a little more in front), and is moving directly away (rightward). Because it begins as close, and is filling a lot of the listener’s auditory field, three different note directions apply, c, e, and g. Together they make the G major chord. That is, by playing a G chord with the individual notes positioned where they are, the listener can recognize via the total sound where the object’s extent is, that it’s on the right but extended a long way from my front to my back, that it’s therefore nearby (supposing it’s a typical everyday object size), but also that it’s moving directly away.
Perception of Stationary Objects While Moving
Thus far, the idea of using chords to cue a blind person about directions of movement was being applied to the movement of other objects.
But probably the most important application of this idea concerns perception of one’s own self-motion among stationary objects, i.e., just navigating the environment and any obstacles. Unlike objects that are moving, stationary obstacles tend to make no sound at all, and blind people would be most aided by being able to hear their (silent) position and movement directions relative to the listener.
When you’re moving forward, everything in the environment moves with the opposite of your velocity (relative to you).
For self-motion, although the same basic principles we already discussed still apply, there are some elegant features here actually making it much simpler.
First and foremost, because the motion here is just self-motion, the Circle of Thirds gets a fixed orientation relative to your direction of movement. That is to say, now each note is not only indicating a direction of movement, but is also indicating a specific spot in your projective field. See Figure 19.
So, for this use case, each note tells you WHERE and WHICH MOVEMENT DIRECTION. These were dissociated for the perception of other movers. A device able to accommodate the movement of objects (as we discussed earlier) needed to be able to play any of the seven notes in any part of your projective field.
But a device able to accommodate self-motion needs to only have a dedicated “d” sound at the front of your head (via a hat or helmet), a dedicated “b” sound to the front right, and so on. Each note will only activate if there’s some object (or part of an object) in the environment in that direction (see Figure 19). The note’s loudness will be according to its distance (inverse square). (I’m assuming here that the mover’s head is always facing in the direction of motion, which of course won’t always be the case.)

Objects in the environment will be heard as chords, i.e., groups of notes that are adjacent within the Circle of Thirds.
Larger or nearer objects will be heard as larger chords.
The chords will tend to progress from d to e (right side), or from d to c (left side). (Choice of which side is which is arbitrary.)
The chords will tend to begin as small, get larger, and then eventually become small once well past it.
There might well be multiple objects, in which case there might be two simultaneously played chords from disparate parts of the circle. The result should be dissonant, but sound potentially like two distinct chords, rather than a single uninterpretable messy sound.
For example, for the example in Figure 20, at that moment both the b and d notes would be played, each at their respective positions in the projective field display in the helmet.
A fraction of a second later and that same object on the right might be played as an Em (see Figure 21). But, perhaps there’s also now some other approaching object, on the left, and so, in addition to Em being played, f is also played. There might be lots of other objects farther away that are detected by the device, but their loudness will be so low as to effectively be silent.
If you’re walking straight, the chord progressions for the stationary objects in the environment will tend to be along one of the two sides. When far away, those progressions look like one of those below, where d is optional
[toward] d, b, g, e [away]
[toward] d, f, a, c [away]
When one passes the object fairly closely, it will instead tend to look more like
[toward] d, d-b, b-g, b-g-e (Em), g-e, e [away]
[toward] d, d-f, f-a, f-a-c (F), a-c, c [away]
But you may well move in interesting trajectories, turning in order to encounter some object, passing it, turning again for another pass, and so on. The result would be repeated loops in this space, i.e., chord progressions going around the Circle of Thirds.
One might wonder why it’s useful to have different musical notes for each of the seven positions around the walker. After all, if each note is at a unique position, why can’t each note just be the same sound? …and we then determine the where from spatially locating which of the seven stimuli are active?
First, our ability to spatially locate via sound isn’t great. But if each location has a unique note, that makes the auditory cue for the where much less ambiguous.
Second, although in this special self-motion case the where and the movement direction are tightly locked together (unlike in the general case), we still have the problem of how to find ways for the various distinct auditory to combine and be perceptually grasped as a single entity. In fact, we still have all the same eight criteria we laid out earlier that we want the stimuli to satisfy. And using the Circle of Thirds in the way I have described still satisfies those requirements.
Summary
What appeared to be a suspiciously simple idea for cuing movement directions of objects (use the Circle of Thirds, with the activation of the note d meaning “toward me”) turns out to be very powerful. It has the key properties needed to work to cue the movement of objects, including that they have parallax (cued by combinations of adjacent notes in the Circle of Thirds, which includes chords with which our brains are familiar), and that a moving object courses through multiple such states during its path (cued by sequences of chords, i.e., chord progressions, something with which our brains are also familiar).
This is just to say: Chords and chord progressions, the basic backbone of music as we all know it, serves to indicate the parallax-filled movements of objects in our midst. And, as the most important special case, serves to help blind people “see” the silent stationary objects in their environment.





